New tutorials
Hereby some recommended new tutorials to learn programming in NetLogo. The first one is from the NetLogo team. It provides a beginner’s guide to NetLogo programming. The other tutorial is
This textbook provides a practical introduction to agent-based modeling using NetLogo based on 15 years of teaching this methodology to students in the life and social sciences. Agent-based modeling is increasingly used by social and life scientists in their research and teaching. Agent-based modeling is discussed in this book as a research tool in tandem with other methodologies, as such attention is given to modeling as a scientific method.
The book first describes basic concepts and introduces you to NetLogo. Then gets you more familiar with modeling and NetLogo by exploring several classic agent-based models. Further, we discuss methods to analyze models using sensitivity analysis and calibration. We close with a series of chapters on ecosystem management and diffusion of viruses and gossip in networks.
Each chapter uses practical examples with NetLogo models, and those models are part of the standard NetLogo software or are freely available in the Computational Model Library of Comses.net.


The book was created as an ebook to allow for interactive links to follow up material, including videos, and the models described in the book. You can read the ebook on your iPad, desktop computer, and mobile phone and interact with some of the models in the web version of NetLogo. Available as EPUB (Apple Books) and KINDLE (Amazon) book.
Marco A. Janssen is a professor in the School of Sustainability and director for the Center for Behavior, Institutions, and the Environment (CBIE). Dr. Janssen received a master’s degree in Operations Research (1992) at Erasmus University Rotterdam, the Netherlands, and a Ph.D. in Mathematics (1996) at Maastricht University, the Netherlands. Since the early 1990s, Dr. Janssen has applied computational modeling to study social, ecological, and social-ecological systems at local, regional, and global scales. Dr. Janssen has published more than 200 peer-reviewed scientific articles in international journals, including Science, Nature, Proceedings of the National Academy of Sciences USA, Global Environmental Change, Ecology & Society, Ecological Economics, Current Anthropology and the Journal of Artificial Societies and Social Simulation.
Currently, Dr. Janssen is co-Editor in Chief of Ecology & Society and President of the International Association for the Study of the Commons. He also co-directs the Network for Computational Modeling in Social and Ecological Sciences.
Hereby some recommended new tutorials to learn programming in NetLogo. The first one is from the NetLogo team. It provides a beginner’s guide to NetLogo programming. The other tutorial is

A new version of the book is out in time for the Fall semester! Due to requests to have the book available on multiple types of devices, we reimplemented the
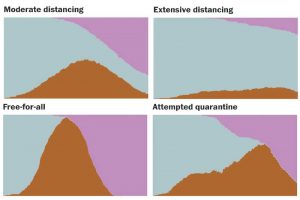
Agent-based model demonstrates how social distancing flattens the curve of corona virus cases.
When you purchase this ebook, you are entitled to all future update versions. By registering here you will be notified of future releases.